아직 갈길이 멀지만 Computer Vision에 대해 관심이 많아서 디퓨전 모델에 대한 논문을 리뷰해보려고 한다. 이걸 시작으로 앞으로 CV쪽 논문에 대해서도 정리를 해보려고 한다.
Learned
1. 생성 모델 특히, 이미지 생성모델에 대해서 전반적으로 파악하고 비교할 수 있었던 논문.(데이터 분포와 이를 추정하는 접근 방식에 대한 내용이 인상깊었다. 특히 DBMS 연구실에서 정리해주신 도식이 명확하게 한눈에 각 모델의 차이를 이해하기 좋았다.)

2. Diffusion 모델이 실제로 수학적으로 어떻게 작동하는지 원리에 대해서 배우면서 각 개념들에 대해서 좀 더 단단하게 이해할 수 있었다. 특히 마코프 체인의 특성과 가우시안 분포를 활용해서 문제를 단순화하는 것이 인상깊었다.
3. Tractable한 분포가 무엇인지에 대해서 이해하느라 엄청 오래걸렸는데 궁극적으로 그 뜻에 대해서 잘 이해할 수 있었음
Summary

Denoising Diffusion Probabilistic Models(Jonathan Ho. 2020)
사전 지식
논문에 있는 내용은 아니며, 꽤 최신의 논문이다 보니 그동안의 문제와 해결책들을 모두 알고 있어야 해서 이번 논문을 이해하는데 있어서 필요한 사전 지식들을 정리해보았다.
Generative Model의 기본적인 접근

- 이미지 데이터(학습 데이터)를 보고 이와 유사한 사진들을 생성하는 모델을 만들고 싶다고 하자. 이러한 이미지를 생성하는 방법으로 여러가지 방법이 있겠지만 이미지 데이터의 확률 분포를 우리가 알 수 있다면 그 분포를 가지고 유사한 이미지를 생성할 수 있을 것이다.
- 즉 생성모델을 만드는 것 = 학습데이터의 p(x)와 생성모델을 통해 만든 데이터의 P(x)의 차이를 줄이는 것과 같고 이를 학습하면 된다.
Generative model의 분류

- 그렇다면 우리는 분포를 어떻게 찾을까?
- 사실 분포는 찾는 것이 아니라 일종의 가정을 하는 것이다. 가설 검정처럼 이러한 데이터들을 봤을 때 어떤 분포를 따를 것이다라고 전제를 세우는 것이다.
- 이 때 우리는 실제 훈련 데이터의 분포를 정의할지 여부에 따라 Explicit(참고하는 쪽) density와 Implicit density(참고 X)로 나눌 수 있다. density는 확률 분포라고 생각하시면 된다.
- [Explicit] Tractable density : 직접적으로 학습데이터에서 바로 배우는 방식이고, 명확하게 확률분포로 계산할 수 있는 방식
- [Explicit] Approximate density : Tractable 방식의 경우 복잡한 데이터 분포를 학습시키기 어렵거나 불가능한 경우로, 이 때는 더 간단한 확률분포로 근사하여 접근하는 방식이다.
- [Implicit] Direct : 샘플링 방식과 같이 실제 분포를 정의하지 않은 채로 생성한 값의 분포와 실제 결과값의 분포 차이를 비교하는 방식
- 이걸 이해하는데 굉장히 오랜 시간이 걸렸는데 내가 이해한 언어로 다시 정리해보면 이와 같다.
- 생성 모델의 본질은 우리가 만들려는 이미지의 분포와 우리의 모델이 만들어내는 이미지의 분포가 같을 확률을 높이는 것이다.
- 이를 해결하기 위해 우리는 어떠한 X가 확률분포를 통해 학습데이터를 만들어낸다고 가정하고 이 확률분포를 배우는 것이 Explicit 접근 방식이다.
- 이 때, 이 특정 분포가 연산하기 쉬운(Tractable) 분포로 가정할지, 아니면 실제로 tractable한 분포로는 도저히 이 데이터 분포를 설명하기 어려울 경우에는 intractable한 분포로 가정을 할 수밖에 없다.
- 이걸 우리가 한번에 결정하기는 어렵고 다양한 EDA를 통해서 파악해야한다. 대부분, 복잡한 패턴을 가진 데이터(음성, 시각, 그림)는 사실 tractable한 분포로 가정하기 어렵다.(가우시안 분포, 베르누이 분포가 Tractable한 분포의 예시)
- tractable한 분포는 말그대로 연산하는 과정이 쉽다는 장점이 있지만 실제 우리 현실에서의 데이터들이 이 분포를 따른다고 가정하려면 여러가지 전제조건, 제약사항들이 많이 따라서 사실 활용하기 쉽지 않다.
- intractable한 접근 방식은 분포를 찾거나 연산하기 어렵기 때문에 연산하기 쉽고 최적화할 수 있는 형태로 근사화하는 것이 문제의 핵심이다.
- 이 때, 이 특정 분포가 연산하기 쉬운(Tractable) 분포로 가정할지, 아니면 실제로 tractable한 분포로는 도저히 이 데이터 분포를 설명하기 어려울 경우에는 intractable한 분포로 가정을 할 수밖에 없다.
- 반대로 Implicit한 방식은 확률 분포은 가정하지 않고, 그냥 모델이 어떻게든 만들어내는 결과물이 실제 데이터와 유사한지만 보는 방식이다.
용어 정리
- 디퓨전 : input 이미지에서 이미지 데이터 분포와 독립적인 Noise를 만들기 위해 단계별로 조금씩 노이즈를 추가하는 것
- Sampling : 구한 확률분포를 활용해서 데이터(이미지)를 만들어내는 과정
- Gaussian : 이미지 -> 디퓨전 과정에서 추가하는 노이즈의 데이터 분포가 가우시안 분포를 따른다.
- Variational Inference(변분 추론) : 확률적 모델링(확률분포를 찾는 것)에서 사후 분포를 찾는 것이 어려울 때 이를 근사화하는 기법 중 하나이다. 복잡한 사후 분포 대신에 간단하고 tractable한 파라미터로 이루어진 분포로 근사해서 문제를 최적화 문제로 바꿀 수 있다는 점이 핵심이다.(최적화 => 경사하강법으로 풀 수 있다.)
- Langevin dynamics : 샘플링을 하면서 noise -> 실제 이미지로 넘어가는 과정이 필요한데 이 때의 데이터 분포를 langevin dynamics의 분포를 활용했다.
- 잠재변수 모델(latent variable) : 관찰 가능한 데이터(X, 학습 데이터)에서 직접 측정할 수 없는 '잠재 변수'를 이용해 모델을 구성하는 방식이다. 잠재 변수는 직접 관찰되지 않지만 관찰 가능한 데이터의 분포를 설명하는 데 중요한 역할을 하는 변수이다. 잠재 변수 모델은 관찰 데이터의 분포를 효과적으로 설명하고 복잡한 패턴을 파악하는 데 널리 사용된다 PCA, FA같은 것도 일종의 특성을 뽑아내는 방식이라고 볼 수 있다. 우리가 이미지를 생성하려면 그 구성요소나 이미지 안의 특징을 잘 뽑아내야하는데 여러 픽셀들의 데이터 속에서 잠재 변수를 뽑아내고 이를 이미지 생성에 활용하기 위한 목적으로 잠재변수 모델을 잘 활용된다.
- 사실 오늘날 모델들에서 사용하는 z는 가우시안분포와 같이 아주 단순한 분포를 특정한 패턴을 가지는 분포로 변환시키는 것을 목표로 한다.(백지에서 원하는 그림을 만들어내는 접근). 그렇기에 대부분의 생성보델이 주어진 입력데이터로부터 latent variable(Z)를 얻어내고 이를 변환하는 역량을 학습시키는 것이 생성 모델들의 주요 접근 방식이다.
- 반대로 autoregressive 모델이 있는데 이는 자기 자신을 input으로 다음 예측을 하는 일종의 RNN이 autoregressive모델이라고 볼 수 있다.
서론
최근 다양한 종류의 생성모델들이 다양한 데이터 모달리티에서 고품질의 샘플을 성공적으로 생성하고 있다. GAN, autoregressive models, flow, VAEs는 현저하게 좋은 이미지와 오디오 샘플을 만들어냈고 그 이면에는 에너지 기반의 모델링과 스코어 매칭의 접근법의 발전이 있었다.
이 논문은 diffusion probabilistic model(이하 디퓨전 모델)의 개선 버전에 대해 설명한다. 디퓨전 모델은 일정한 시간 이후의 데이터와 유사한 데이터를 만드는 variational inference를 사용하여 학습된 파라미터로 이루어진 Markov Chain이다.
일반적으로 원본 이미지에서, 이미지가 가진 정보가 모두 사라질 때까지 데이터에 노이즈를 추가하는 것이 디퓨전 프로세스이며 이 프로세스의 역행하는 방향으로 학습된 모델이 디노이징 프로세스이며 이 역시도 마코프 체인이다. 디퓨전이 소량의 가우시안 분포에 있는 노이즈를 더해가면서 생성되므로, 샘플링 체인 역시 조건부 가우시안 분포를 이룬다고 볼 수 있으며 이는 신경망으로 표현할 수 있다.
Background
DDPM으로 가기 전에 실제 수식과 각각의 프로세스를 다시 정리해보았다.
우선 알아야하는 특징은 총 4가지이다.
1. 각각의 프로세스는 모두 마코프 체인 성격을 따른다. 이는 오로지 현재(t)의 상태는 직전 시점(t-1)의 상태를 따른다.
2. Diffusion Process(원본 이미지에 노이즈를 더하는 작업)는 VAE와 다르게 학습 대상이 아니며, 가우시안 분포를 따르는 노이즈를 조금씩 더해가면서 다음 상태를 바꾼다.
3. 학습 단계에서 이미지의 크기(dimension)가 바뀌지 않도록 만들기 위해 우리는 x(t) = √{1-b(t)} * x(t-1) + b(t) 로 고정해서 연산한다. 여기에서 b는 분산을 의미하며 이번 실험에서는 이 분산을 0.0001 ~ 0.04로 차차 수정시켜가면서 최종적으로는 x(t)에서는 평균과 분산이 각각 (0,1)을 가지는 가우시안 분포에 가까워지도록 만들었다. (논문에서는 이를 variance schedule이라고 얘기한다.)
4. 위 논문은 최대한 수식을 간결하게 만들기 위해서 여러 변수를 다시 정의하는 과정(Reparameterization)이 많다.
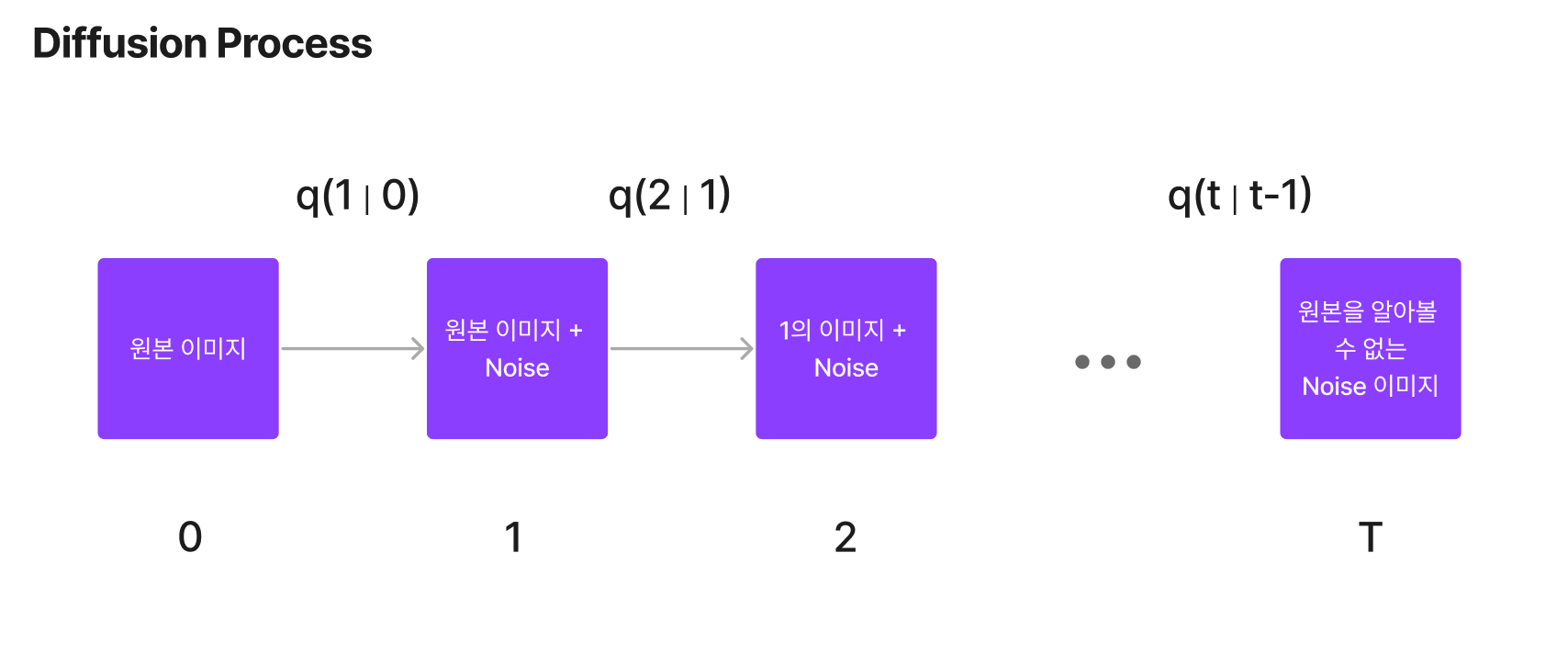
디퓨전 프로세스의 식은 아래와 같이 정의할 수 있으며, 마코프 체인이기 때문에 조건부 확률 분포임을 확인할 수 있다. 조건부 확률 분포를 가지고 단순 노이즈를 주입하는 과정이기 때문에 x0에서 바로 xT를 구할 수 있다. 우측의 식은 위에서 이야기한 variance schedule을 확인할 수 있다.
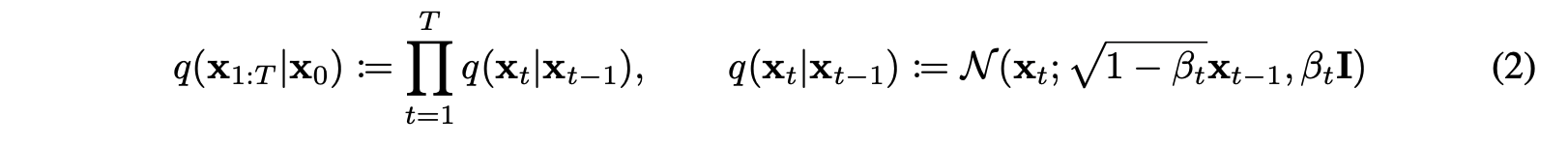
이 때 x(t)를 구하기 위해서 0부터 지속적으로 연산하는 것은 일종의 병목이 발생하지만 이 b(t) = 1- a(t)로 바꿔줌으로써 우리는 x0부터 바로 xt를 빼올 수 있는 확률 분포를 구하는 식을 도출할 수 있다.

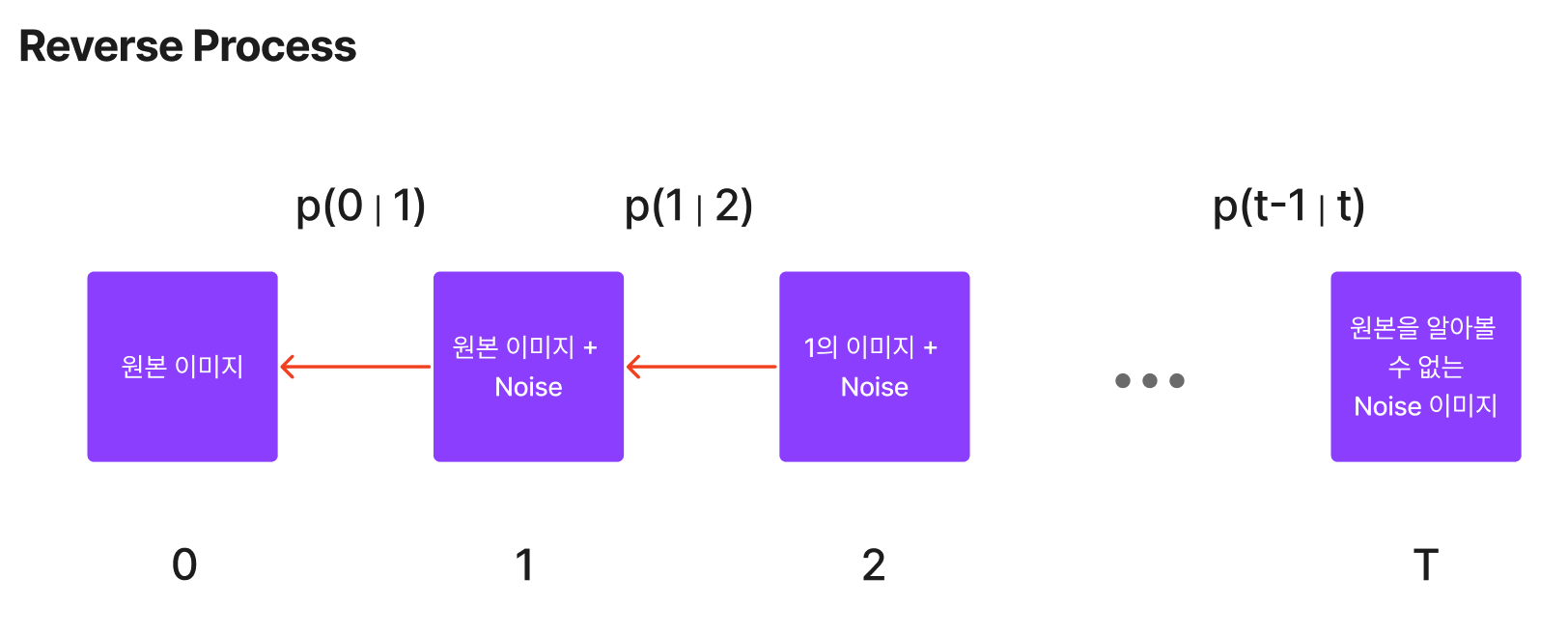
노이즈를 걷어내고 원본이미지를 찾아가는 확률분포를 논문에서는 P로 정의했으며, 이 분포의 모수(평균, 분산)를 찾는 것이 diffusion 모델의 목표다.
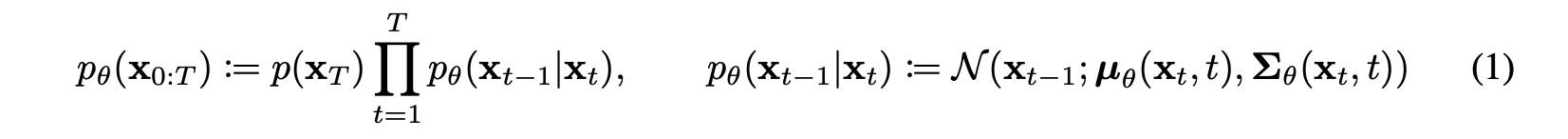
Diffusion Model의 Loss Function
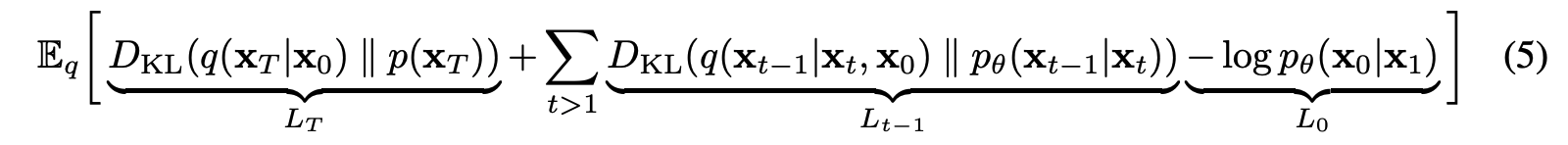
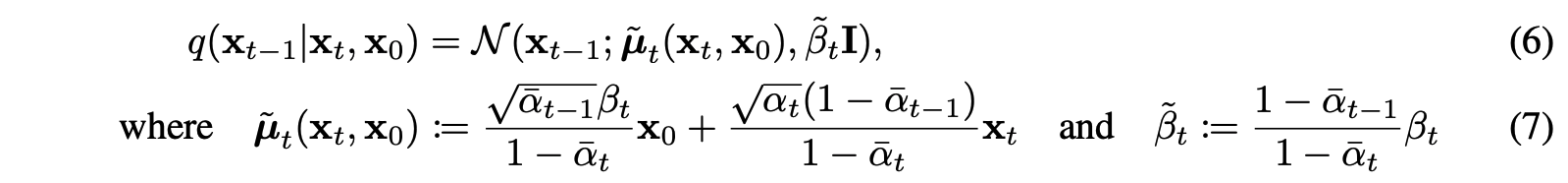
디퓨전 모델의 Loss function의 식은 이렇게 세워볼 수 있다.
Diffusion models and denoising autoencoders
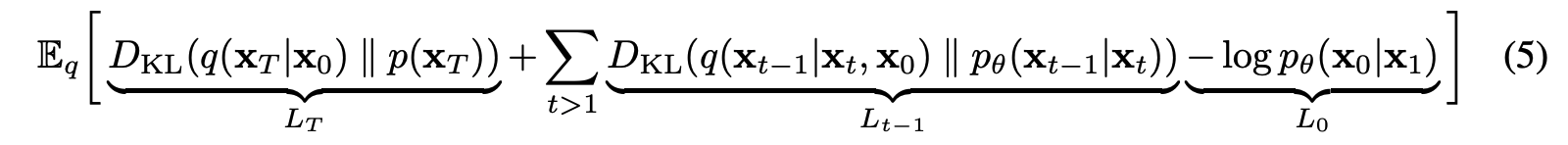
이 논문에서는 이 분산 b(t)를 상수로 함으로써 이 loss function을 단순화하려고 한다.
3.1 Forward process and L(T)
L(t)는 x0부터 시작해서 우리는 가우시안 분포 노이즈를 지속적으로 더해나가며 b(t)를 스케줄링해서 최대한 N(0,I)를 이루도록 Xt를 만들기 때문에 이 로스 펑션은 상수라고 볼 수 있어서 목적함수에 들어갈 필요가 없다.
또한 L(0)로 돌아가보면, x1이 주어졌을 때 x0의 조건부확률분포의 로그를 최소화하는 것은 매우 작은 노이즈를 더해주는 작업이기 때문에 이 또한 제외한다.
3.2 Reverse process and L1:T-1
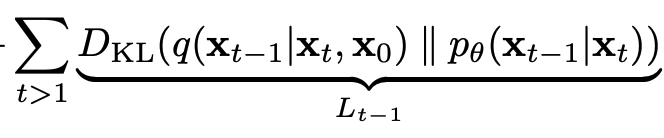
이제 이 식을 간소화해보려고 한다. KL divergence 안의 좌측은 사실 이미 우리가 알고 있는 고정된 상수이고 우리가 구해야하는 것은 우측의 p(theta) 분포이다. 우측은 가우시안 분포로 정의해볼 수 있으며 이 때 우리가 알아야할 평균과 분산을 아래와 같이 표현할 수 있다.
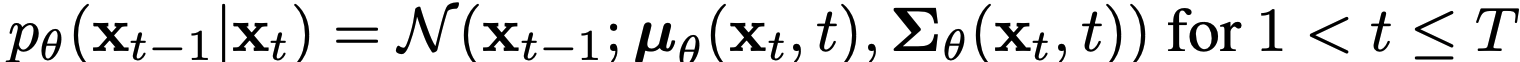
좌측 역시도 가우시안 분포를 따르며 아래와 같이 평균과 분산을 가진다.
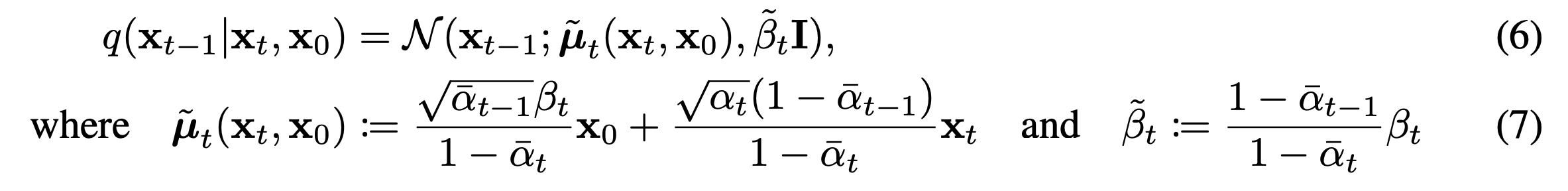
또한 앞에서 우리는 분산의 경우 아래와 같이 표현할 수 있고 이는 상수라고 치환할 수 있다.(시간이 지남에 따라 누적되는 분산이기 때문)
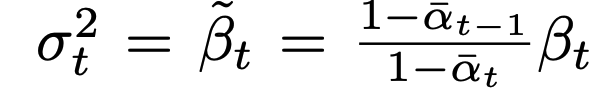
이를 통해 모델이 학습해야할 것은 세타(xt, t)로 표현되는 평균을 구하면 되는 문제로 간소화되었다.
다시 Loss function을 정리해보면 아래와 같다.
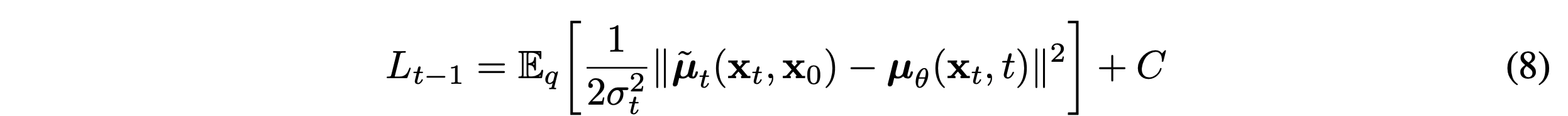
이제 이 Loss function을 풀어서 쓰면 아래와 같다.

3.4 Simplified training objective
여러 전제를 통해서 목적함수를 많이 생략했는데 생략한 조건을 포함시켜서 같이 트레이닝시킨 후 비교했을 때 큰 차이가 없음을 확인할 수 있었다.
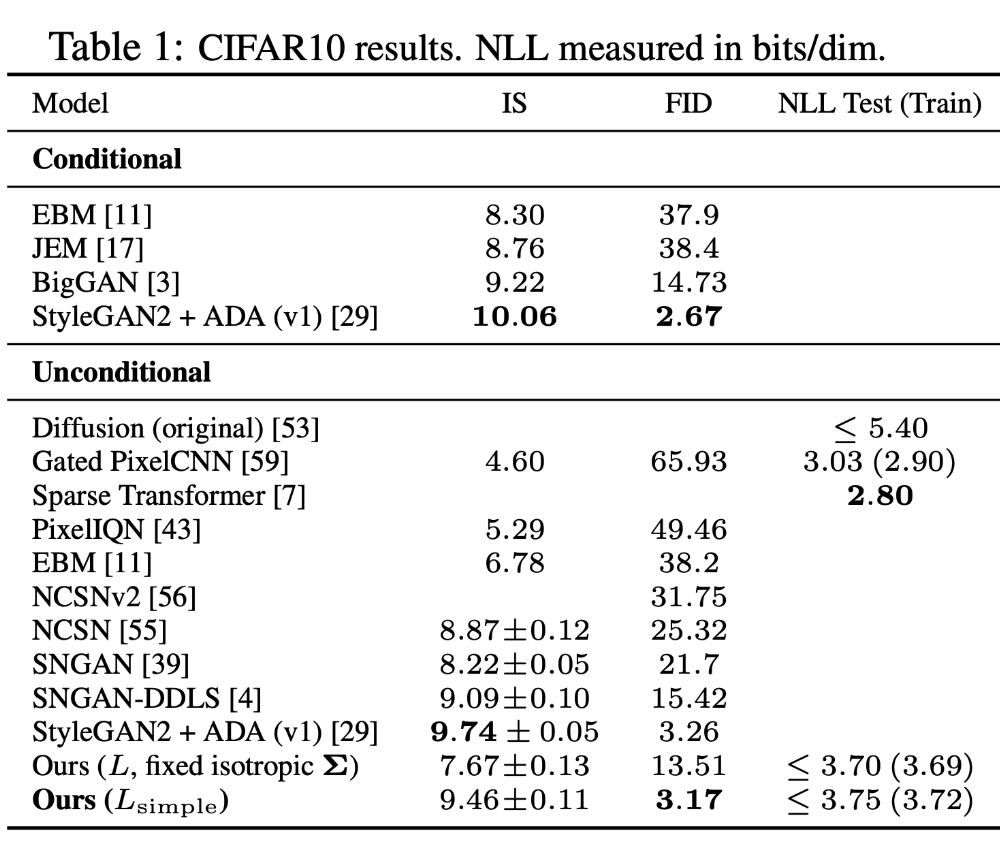
Experiments
4.1 Sample Quality (모델이 생성해내는 이미지의 퀄리티)

4.2 Reverse process parameterization and training objective ablation (L(T-1))
평균을 예측하는 것이 아니라 엡실론을 예측함에 대한 결과는 나쁘지 않게 나옴을 확인할 수 있었다.
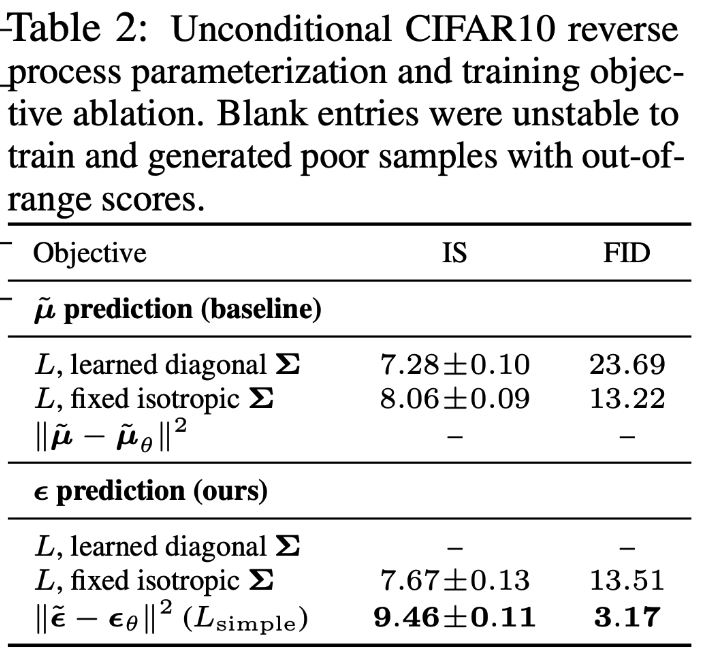
4.3 Progressive coding

Related Work
디퓨전 모델이 일부 Flow(함수와 역함수를 활용)와 VAEs(encoding과 decoding)와 유사하긴 하지만 실제로 디퓨전 모델은 q(노이징 하는 함수)의 parameter가 없고, X(t)와 X(0)가 전혀 관계없는 상태라는 점이다.
파라미터를 수정해서 학습시켜야할 대상을 엡실론 학습으로 바꿈으로써 우리는 Denoising score matching과 디퓨전 모델과의 관계를 정리할 수 있었다.
Conclusions
우리는 디퓨전 모델을 활용해서 고화질의 이미지를 만들 수 있었고 여러 생성모델(energy-based model, denoising score matching, 디퓨전 모델)간의 관계를 정리할 수 있었다.
끝으로 이해안되는 부분은 영상도 보고 블로그도 찾아보고 했는데 많이 도움되었던 블로그도 링크로 걸어둔다.
2. https://www.youtube.com/watch?v=_JQSMhqXw-4
3. https://hyoseok-personality.tistory.com/entry/Concept-Diffusion-Models-with-DDPM-DDIM
'Machine Learning > 논문 리뷰' 카테고리의 다른 글
| [RLHF] Deep Reinforcement Learning from Human Preference 논문 리뷰 (0) | 2023.09.19 |
|---|---|
| LoRA: Low-Rank Adaptation of Large Language Models 논문 리뷰 (1) | 2023.09.16 |

